哈希游戏作为一种新兴的区块链应用，它巧妙地结合了加密技术与娱乐，为玩家提供了全新的体验。万达哈希平台凭借其独特的彩票玩法和创新的哈希算法，公平公正-方便快捷!万达哈希,哈希游戏平台,哈希娱乐,哈希游戏

　　注意：增量di应具有“完备性”。即：产生的Hi均不相 同，且所产生的s(m-1)个Hi 值能覆盖哈希表中所有的地 址。则要求： ※ 平方探测时的表长m必为4j3的质数； ※ 随机探测时的m和di没有公因子。

　　线性探测容易产生二次聚集，一次聚集的产生主要取决 于哈希函数，在哈希函数均匀的前提下，可以认为没有 一次聚集。

　　设标识符可以用一个计算机字长的内码表示。因为内码平 方数的中间几位一般是由标识符所有字符决定，所以对 不同的标识符计算出的散列地址大多不相同，即使其中 有些字符相同。 在平方取中法中，一般取散列地址为 2 的某次幂。例如， 若散列地址总数取为 m = 2r，则对内码的平方数取中间 的 r 位。如果 r = 3，所取得的散列地址参看下图的最右 一列。

　　对于频繁使用的查找表，希望ASL=0。即不需要从“比较” 的结果来确定查找成功，只有一个办法：预先知道所查 关键字在表中的位置，也就是说，记录在表中位置和其 关键字之间存在一种确定的关系。 例如： 为每年招收的1000名新生建立一张查找表，其关键字为 xx000 ~ xx999(前两位为年份)。则可以下标为000 ~ 999 的顺序表表示之。由于关键字和记录在表中的序号相同， 则不需要经过比较即可确定待查关键字。

　　关键问题是：如何选取 p ? p 应为不大于m 的质数或是不含20以下的质因子

　　例：有一个关键字 key = 962148，散列表大小 m = 25，取 质数 p= 23。散列函数 H( key ) = key % p。则散列地址为 H ( 962148 ) = 962148 % 23 = 12。 需要注意的是， 使用上面的散列函数计算出来的地址范围是 0到 22，因此， 从23到24这几个散列地址实际上在一开始是不可能用散列 函数计算出来的，只可能在处理溢出时达到这些地址。

　　示例：设给定的关键码为 key = ，若存储空 间限定 3 位, 则划分结果为每段 3 位. 上述关键码可划分 为 4段：

　　41 把超出地址位数的最高位删去, 仅保留最低的3位，做为可 239 385 878

　　当散列 38 时发生冲突，同 60 争夺第 5 个单元  解决办法 ：探测下一个空单元，步长：1 H(key) = ( keydi) MOD 11，其中：di 为 1、2……10 注意：可取其它步长，如 3  冲突： 初级冲突：不同关键字值的结点得到同一个散列地址。 二次聚集：同不同散列地址的结点争夺同一个单元。 结果：冲突加剧，最坏时可能达到 O（n）级代价。

　　假设关键字集合中的每个关键字都是由 s 位数字组成 (k1, k2, …, kn)，分析关键字集中的全体，并从中提取分布均 匀的若干位或它们的组合作为地址。 仅限于：能预先估计出全体关键字的每一位上各种数字出 现的频度，它完全依赖于关键字集合。如果换一个关键 字集合，选择哪几位要重新决定。

　　它不同于前面介绍的几种查找方法。 上述方法都是把查找建立在比较的基础上，而哈希查找则 是通过计算存储地址的方法进行查找的。

　　9.3.1什么是哈希表 纵观以上两节讨论的表示查找表的各种结构，有一个共同 点：记录在表中的位置和它的关键字之间不存在一个确 定的关系，因此，查找的过程为给定值依次和关键字集 合中各个关键字进行比较，查找的效率取决于和给定值 进行比较的关键字个数。 因此，用这类方法表示的查找表，其平均查找长度ASL都 不为零，不同表示方法的差别仅在于：和给定值进行比 较的关键字的顺序不同。

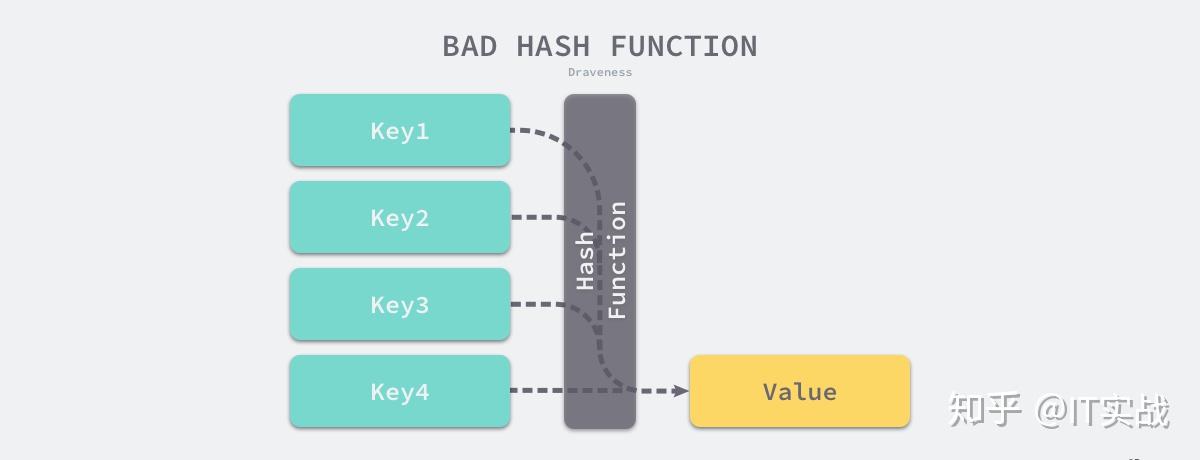
　　从这个例子可见， 哈希函数是一个映象，即：将关键字的集合映射到某个 地址集合上，它的设置很灵活，只要这个地址集合的大 小不超出允许范围即可; 由于哈希函数是一个压缩映象，因此，在一般情况下， 很容易产生“冲突”现象，即：key1 key2，而 f(key1) = f(key2)。并且，改进哈希函数只能减少冲突，而不能 避免冲突。 因此，在设计哈希函数时，一方面要考虑选择一个“好” 的哈希函数;另一方面要选择一种处理冲突的方法。

　　所谓“好”的哈希函数，指的是，对于集合中的任意一个 关键字，经哈希函数“映象”到地址集合中任何一个地 址的概率是相同的。称这类哈希函数为“均匀的”哈希 函数。

　　哈希表：根据设定的哈希函数H(key)和所选中的处理冲突 的方法，将一组关键字映象到一个有限的、地址连续的 地址集(区间)上，并以关键字在地址集中的“象”作为 相应记录在表中的存储位置，这种表被称为哈希表。 所得存储位置称为哈希地址(又称散列地址)。

　　在 处 理 冲 突 的 过 程 中 可 能 得 到 一 个 地 址 序 列 Hi(i=1 ， 2，…，k，hi∈[0，…，n-1])。即在处理哈希地址的冲 突时，若得到的另外一个哈希地址Hi任然发生冲突，则 再求下一个地址H2 ，若H2 任然冲突，再求得H3 。依次 类推，直至Hk不发生冲突为止，则Hk为记录在表中的地 址。

　　此方法把关键字自左到右分成位数相等的几部分，每一部 分的位数应与散列表地址位数相同，只有最后一部分的 位数可以短一些。把这些部分的数据叠加起来，就可以 得到具有该关键字的记录的散列地址。 有两种叠加方法： 移位法—把各部分的最后一位对齐相加； 分界法—各部分不折断，沿各部分的分界来回折叠，然后 对齐相加，将相加的结果当做散列地址。

　　实际造表时，采用何种构造哈希函数的方法取决于建表的 关键字集合的情况 (包括关键字的范围和形态 )，总的原 则是使产生冲突的可能性降到尽可能地小。

　　9.3.2哈希函数的构造方法 对数字的关键字可有下列哈希函数的构造方法，若是非数 字关键字，则需先对其进行数字化处理。 1. 直接定址法 哈希函数为关键字的线性函数 H(key) = key 或者 H(key) = a  key b 如：k1, k2 分别有值 10 、1000；选10、1000 作为存放地 址。 简单、不经济。 仅限于：地址集合的大小 = 关键字集合的大小

　　但是，对于动态查找表而言， 1) 表长不确定； 2)在设计查找表时，只知道关键字所属范围，而不知道确 切的关键字。 因此，一般情况，需建立一个函数关系，以f(key)作为关 键字为key的记录在表中的位置，通常称这个函数f(key) 为哈希函数。 注意： 这个函数并不一定是数学函数。

　　此方法在词典处理中使用十分广泛。它先计算构成关键码 的标识符的内码的平方，然后按照散列表的大小取中间 的若干位作为散列地址。 若关键字的每一位都有某些数字重复出现频度很高的现象， 则先求关键字的平方值，以通过“平方”扩大差别，同 时平方值的中间几位受到整个关键字中各位的影响;

　　解决冲突的方法又称为溢出处理技术。因为任一种散列函 数也不能避免产生冲突，因此选择好的解决冲突溢出的 方法十分重要。

　　9.3.3处理冲突的方法 假设哈希表的地址集为0~(n-1)，冲突是指由关键字得到的 哈希地址为j(0≤j≤n-1)的位置上已存在记录，则处理冲 突就是为该关键字的记录找到另一个“空”的哈希地址。 处理冲突的实际含义是： 为产生冲突的地址寻找下一个哈希地址。